Mastering Logarithms: A Fun Math Challenge with Circles
Written on
Understanding Loga(b) and Circle Geometry
In the realm of geometry, particularly concerning circles, the constant pi appears in various formulas. Today, we will tackle a mathematical challenge where we need to determine the value of an expression using the radius and circumference of a circle.
Do you think you can solve it in under a minute? It’s quite simple! I suggest pausing here, grabbing a pen and some paper, and giving it a try. When you feel ready, continue reading for the solution!
Solution Exploration
Assuming the radius of the circle is denoted as r, the formula for its circumference is 2πr.

At times, the most apparent approach is indeed the right one. Thus, we will substitute r into the formula 2πr.

By simplifying, we can bring down the 2 from ( a^2 ) and the 4 from ( b^2 ).

Next, we eliminate the 4s, allowing us to rearrange the equation to find ( frac{log_{10}(b)}{log_{10}(a)} ).
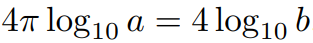
And there you have it—our final answer!
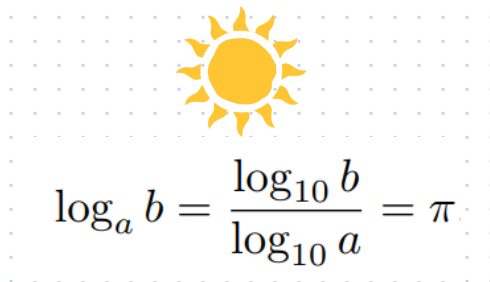
How fascinating is that?
What were your thoughts during this challenge? Please share in the comments; I’d love to hear your insights!
Engaging Video Resources
To further enrich your understanding of logarithmic properties, check out these insightful videos:
The first video demonstrates the proof that ( log_a(b) cdot log_b(a) = 1 ), which is a fundamental property of logarithms.
The second video provides a clear explanation of the logarithmic identity ( log a + log b = log(ab) ), which is essential for algebraic manipulations.
Join the Math Community
Don’t forget to share this engaging math puzzle with friends and encourage them to join in on the fun!
Bella’s Weekly Math Games
Participate in a 48-hour math competition that occurs weekly!
Thank you for taking the time to read this article. If you found it helpful, please consider showing your support!

If you wish to connect professionally or simply want to say hi, feel free to reach out. I would love to chat!
Happy Solving, Bella