Carl Friedrich Gauss

The application of modular arithmetic spans various fields of mathematics, including group theory, field theory, number theory, and p-adic theory. This concept was introduced by Carl Friedrich Gauss in the early 19th century when he was just 21 years old. His seminal work, "Disquisitiones Arithmeticae," was the first to systematically formalize the idea of residue classes, a fundamental aspect of modern number theory.

To illustrate modular arithmetic in a tangible way, consider its relation to clocks. Often referred to as "clock arithmetic," this concept allows us to solve practical problems. For instance, if the hour hand points to 9, and we want to find out where it will point after 28 hours, we can simply take the remainder of 28 when divided by 12, which equals 4. Adding this to 9 gives us 1 o'clock.

Defining Modular Arithmetic

To establish a formal definition of modular arithmetic, we introduce the concept of congruence. Two integers, a and b, are said to be congruent modulo n if n divides the difference between them.

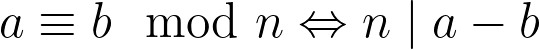
Let’s consider the numbers 66 and 21 and analyze their congruence under modulo 5. Every integer a can be uniquely represented in the form:

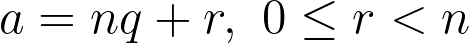
For our example, we can express 66 and 21 as follows:

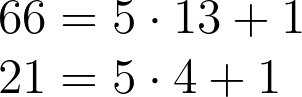
Calculating the difference between these two numbers reveals that their remainders cancel out, resulting in a number that is divisible by 5.

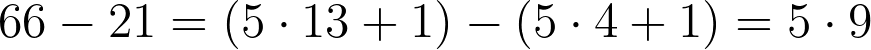
Thus, we conclude that two numbers are congruent modulo n if they yield the same remainder when divided by n. This principle can be applied to any pair of integers to assess their congruence.

Properties of Congruence

We can define a relation among integers based on congruence, which exhibits three key properties:

1. Reflexive: Any integer a is congruent to itself.
2. Symmetric: If a is congruent to b, then b is congruent to a.
3. Transitive: If a is congruent to b and b is congruent to c, then a is congruent to c.

A relation that possesses these properties is termed an equivalence relation, allowing us to partition the set of integers into equivalence classes. Each class can be identified by its remainder when divided by n. There are precisely n distinct remainders, leading to n equivalence classes. We denote the equivalence class of a number a as [a], with n specified by context.

The mapping from an integer a to its corresponding equivalence class [a] functions as a homomorphism, preserving operations through the mapping. This idea may seem daunting, but it merely indicates that the function maintains the structure of operations.

Next, we explore the implications of this function through polynomial equations.

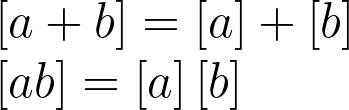
Consider a polynomial equation that has a solution in integers. Applying our mapping, we can express the solution in terms of residue classes. For instance, let’s set n to 2 and apply our mapping to the polynomial equation.

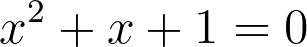
At first glance, the equation appears unchanged; however, [x] can only take on n values. In this case, since n equals 2, we can substitute all potential values of [x] to check for equality. If no values satisfy the equation, it indicates that the original equation lacks integer solutions.

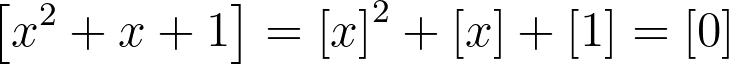
This example may not be particularly revealing since we could solve it using standard methods, confirming that no solutions exist even among real numbers. Let’s examine a more intriguing case: find integers a and b such that:

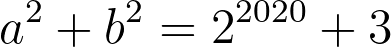
We can reapply our function with n set to 4 to determine if this aids our solution process.

By substituting every possible value of [a] into the left side, we find:

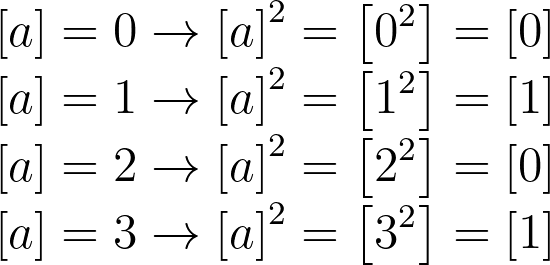
Ultimately, we discover there are no combinations of [a] and [b] that yield [3] as a sum, indicating this equation cannot have integer solutions.

Utilizing modular arithmetic can significantly reduce the number of trials needed to reach a conclusion. In our next discussion, we will apply this technique to demonstrate the absence of rational points on the circle with a radius of the square root of 3.