Understanding Why Zero Raised to Zero Equals One
Written on
Chapter 1: Introduction to Zero Exponentiation
In this discussion, we shift our focus from physics to the intriguing world of mathematics. The concept of zero raised to the power of zero, which equals one, is often puzzling. Let's delve deeper into this topic together!

Section 1.1: The Definition of Exponents
At first glance, the assertion that zero raised to the power of zero equals one may seem to challenge the fundamental definition of exponents. To clarify, when we say X raised to the power of Y, it signifies multiplying X by itself Y times. For instance, X³ = X × X × X.
It’s important to remember that multiplying by zero always yields zero. Therefore, any positive exponent of zero will also result in zero. For example, 0^5 = 0 × 0 × 0 × 0 × 0 = 0. The question then arises: from where does the value of one originate?
Section 1.2: A Graphical Perspective
To visualize this, let’s examine a sequence of numbers: 4, 3, 2, 1, 0.9, 0.8, 0.7, 0.6, 0.5, 0.4, 0.3, 0.2, 0.1, 0.01. By plotting the function y = x^x, we can calculate and record the corresponding y values for each x.
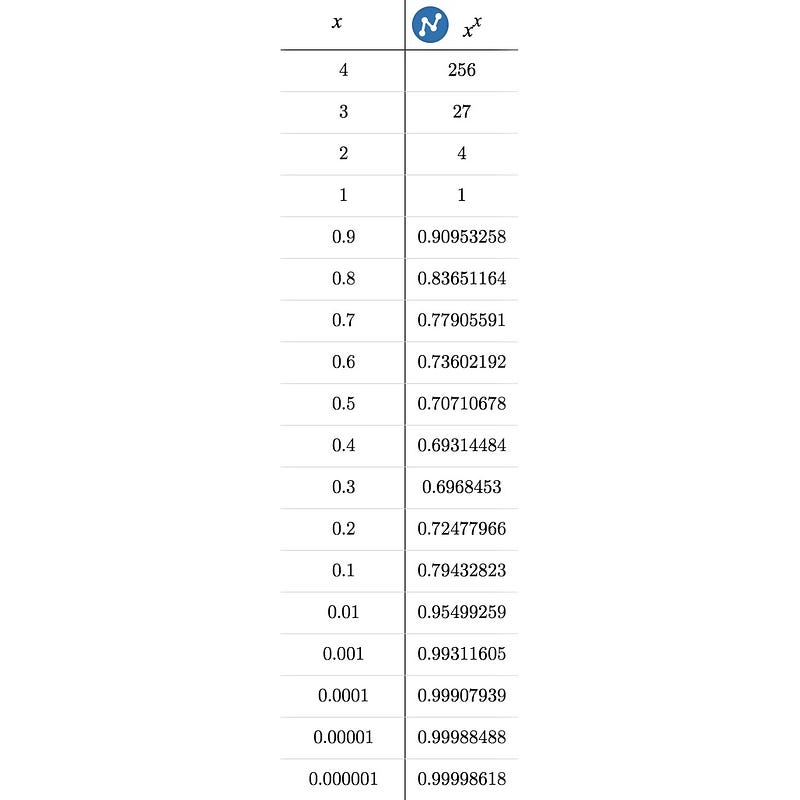
Initially, the values of y decrease as x increases. However, as we approach zero, around x = 0.3, we observe a surprising trend: the values start to rise, and as we near zero, the function approaches one asymptotically.
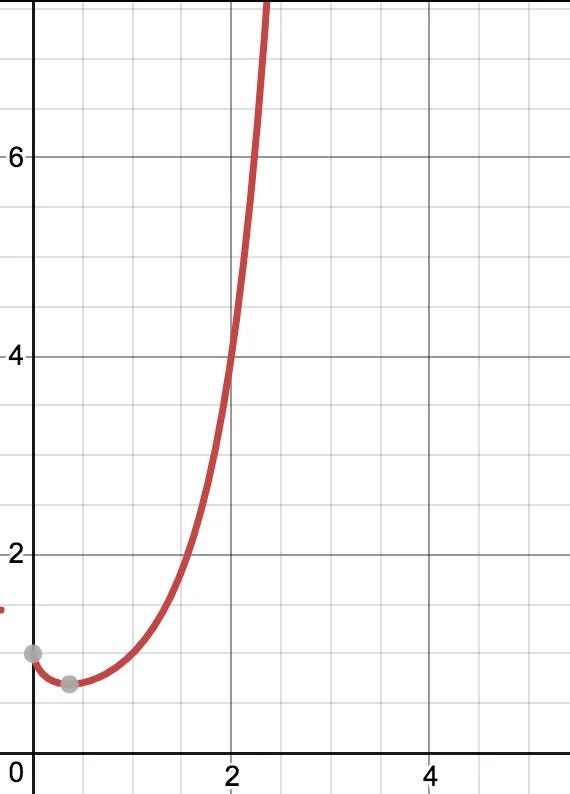
Despite the fact that the function y = x^x is technically discontinuous at x = 0, many branches of mathematics accept the convention that zero raised to the power of zero equals one. This agreement simplifies numerous calculations across various fields, including arithmetic, combinatorics, and set theory.
Chapter 2: The Nature of Zero to the Power of Zero
In higher mathematics, particularly in mathematical analysis, the value of zero raised to the power of zero is often considered indeterminate. Each situation requires analytical resolution, typically through the limit of the natural logarithm of an expression that involves this exponent.
The first video titled "Why does 'x to the zero power' equal 1?" delves into the reasoning behind this mathematical principle, making complex concepts more accessible.
Another insightful video, "What is 0 to the power of 0?" further explores the implications and interpretations of this intriguing topic.
If you're interested in more discussions about mathematical concepts, feel free to subscribe to our channel and engage with your questions, which I'll address in future articles. If you enjoy my content, consider supporting me by becoming a member of Medium for just $5 a month, helping us enhance our offerings.