Chapter 1: The Basics of Negative Numbers

The rule that multiplying two numbers with different signs results in a negative outcome, while multiplying two numbers with the same sign results in a positive one, is well-known. However, many students have pondered why multiplying two negative numbers gives a positive result. Often, this concept is left unexplained in classrooms, leading students to accept it without question. In this article, we will delve into the reasoning behind the idea that a negative multiplied by a negative equals a positive.

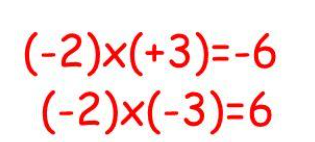
To grasp this concept, let’s trace the logic from its origins. In ancient arithmetic, negative numbers were nonexistent, and all operations were developed to facilitate trade. Picture this scenario: you work for 5 days, earning $10 each day. Your total earnings would be calculated as 10 + 10 + 10 + 10 + 10 = 50, or in multiplication terms, 10 * 5 = 50 dollars. This is how multiplication emerged as a shorthand method for addition.

Now, let’s say you visit a store and purchase items worth $60. You and the shopkeeper agree that you owe him the remaining $10, which he documents as a note indicating your debt. Consequently, your balance would be 50 - 60 = -10 dollars. This illustrates how negative numbers can represent amounts owed. If this scenario repeats the following week, you would find yourself with a debt of 2 * (-10) = -20 dollars, showing that multiplying a positive by a negative results in a negative, as it effectively sums multiple debts.

Suppose a week later, after working another five days, your account balance is -10 + 5 * 10 = 40 dollars. When you meet the shopkeeper, he offers to forgive your debt instead of requiring payment. This can be expressed as 40 - 1 * (-10), as you are relinquishing one note of -10 dollars. Logically, this would leave you with a balance of 50 dollars. Hence, the expression implies that -1 * (-10) equals +10. From such real-life situations, the conclusion emerged that the product of two negatives results in a positive.

Let’s also examine this from a mathematical perspective: when negative numbers were incorporated, mathematicians aimed to ensure that operations applicable to natural numbers would also hold for negative numbers. One such operation is the distributive property: c * (a + b) = c * a + c * b, valid for any natural numbers. Now, let’s see how this applies to integers (natural numbers + 0 + negatives). Consider the expression -3 * (6 + (-6)); expanding it gives -3 * 6 + (-3) * (-6). We already understand that a negative multiplied by a positive results in a negative, yielding -18 + (-3) * (-6). Calculating without expanding, we find -3 * (6 + (-6)) = -3 * (6 - 6), which is -3 * 0 = 0. Thus, to maintain balance, the product of (-3) * (-6) must equal 18.

Therefore, the assertion that a negative multiplied by a negative results in a positive is not merely a mathematical convention; it is rooted in logical reasoning.

This video titled "Why is the product of two negative numbers positive? Math Foundations" explores the foundational principles behind this arithmetic rule. It provides additional insights and illustrations that enhance understanding.

In "Why Are Two Negative Numbers Always Positive When Multiplied?" the video breaks down the concept further, offering examples and explanations to clarify why this rule holds true.

If you wish to see more articles about mathematics and its applications in everyday life, don’t forget to subscribe to our channel and leave your questions for future discussions.