Chapter 1: The Genius of Ramanujan

Srinivasa Ramanujan is a name that resonates deeply within the mathematics community. Known for his extraordinary talent, he had little formal education. As a young boy, he demonstrated remarkable aptitude for mathematics by studying "Synopsis of Pure Mathematics" by G. S. Carr, which included 5,000 theorems known at that time. Despite his impressive work, he initially received little recognition. This changed when he reached out to the esteemed mathematician G. H. Hardy, leading to a brief but highly productive partnership in the early 20th century at Cambridge.

Ramanujan was celebrated for his unconventional approaches to mathematics, often bypassing rigorous proof techniques. He claimed that his insights were divinely inspired by the Hindu goddess Namagiri Thayar. As he famously stated, “An equation for me has no meaning unless it expresses a thought of God.” His theorems often took peculiar forms, including infinite series and square roots.

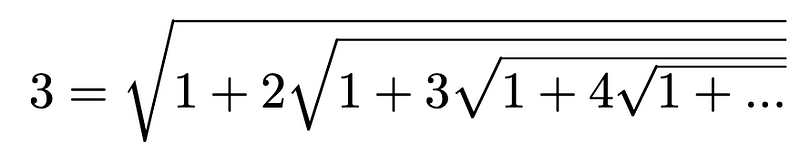
One of his significant contributions was to the Riemann Zeta Function, where he discovered an infinite series representation of it. Tragically, Ramanujan passed away at the age of 32 due to health complications, yet he left behind an astonishing body of work, publishing nearly 3,900 results. Many of his theorems have since been validated, paving the way for entire branches of number theory. Mathematicians continue to delve into his notebooks to uncover more of his genius.

Chapter 2: The Taxicab Number

One of the most intriguing stories about Ramanujan involves the number 1729, which is now famously known as the "Ramanujan-Hardy Number." During a visit to Hardy in England, Ramanujan had to be hospitalized, and Hardy later recounted a conversation about the number of the taxi he rode—1729. He remarked that it seemed quite dull, to which Ramanujan replied, “No, it is a very interesting number; it is the smallest number expressible as the sum of two positive cubes in two different ways.”

This interaction illustrates Ramanujan's extraordinary mathematical insight. Hardy further noted, “Every positive integer was one of Ramanujan’s personal friends.” The number 1729, being the first of its kind in this regard, has led to the concept of Taxicab Numbers.

Section 2.1: Taxicab Numbers Explained

Indeed, Ramanujan was correct; 1729 can be expressed as follows:

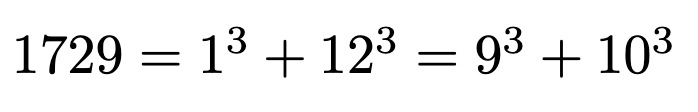
As previously mentioned, 1729 is recognized as the second Taxicab Number, being the smallest integer formed by two distinct cube sums. The third Taxicab Number, as illustrated below, is 8759319, which can be expressed as three different sums of two cubes.

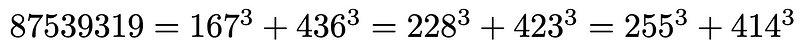
Taxicab Numbers have been identified up to the sixth order, with the values growing rapidly, making it increasingly challenging to find higher-order numbers.

Section 2.2: Understanding Diophantine Equations

Diophantine equations are a central theme in mathematics with a rich historical background, traced back to around 250 CE through the work of the Roman mathematician Diophantus of Alexandria. His book, Arithmetica, introduced 130 such equations, many of which he solved. Diophantine equations refer to any polynomial involving two or more integer coefficients, with solutions required to be integers.

A well-known example of a Diophantine equation is the Pythagorean theorem, which seeks integer solutions known as Pythagorean triples.

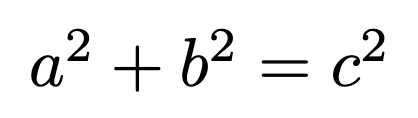
Here are a few solutions to this equation:

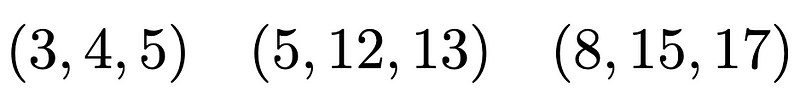
Diophantine equations form the foundation for Taxicab Numbers, expressed generally as follows:

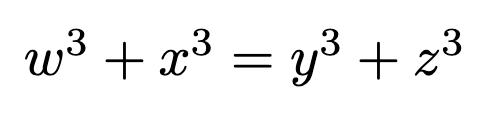
By adding variables to the third power on either side, we can derive higher-order Taxicab Numbers, where the corresponding Taxicab number becomes the smallest integer solution to the equation. The study of Diophantine equations remains a vibrant area of mathematical inquiry.

For those interested in delving deeper into Ramanujan and Diophantine equations, I recommend the film "The Man Who Knew Infinity." While it takes some creative liberties, it remains an engaging portrayal of their collaboration, based on the excellent book of the same title. Additionally, Diophantine equations have gained popularity in math competitions; for a comprehensive introduction, consider "An Introduction to Diophantine Equations: A Problem-Based Approach."

I hope this exploration has enriched your understanding! If you appreciate my work, consider becoming a medium member through this link to show your support. You can also follow me for more stories on mathematics and science, as I publish weekly insights on these topics.