Redefining the 0-Dimensional Point: A Fresh Look at Dimensions
Written on
Understanding the Concept of Zero Dimensions
The notion of a zero-dimensional object can be perplexing. It is typically described as a non-entity existing in a void, devoid of shape or location—essentially, it is pure nothingness. However, our existence and the intricate world around us suggest that there is more to consider.
Have you ever pondered the beginnings of significant events? What triggers a declaration of war? What drives the evolution of a disease like cancer? While you might not have thought deeply about these questions, the instinct to solve pressing problems is a fundamental aspect of human curiosity.
Everything has an origin, be it the Big Bang, the long process of evolution, or even a simple weed sprouting from a seed. Yet, in mathematical terms, the concept of origin is often reduced to a point, or a dot, representing a 0-dimensional object, which remains abstract.
The goal here is to ground this abstraction in reality, establishing a foundational model for problem-solving that connects concepts and perceptions as we step into the first dimension.
Reassessing the Point: Is It Just Old Science?
In my exploration through a multitude of resources ranging from Geometry to Quantum Physics (excluding string theory for the moment), I've come across various interpretations of the 0-dimensional concept. A point serves as a fundamental building block, simplifying complex mathematical calculations in the sciences.
In Euclidean geometry, a point is purely abstract. When multiple points form a line, that line remains abstract as well, representing the first dimension. This line can further expand into a two-dimensional object, akin to a flat piece of paper—an illustration of the second dimension without height or thickness.
When we introduce height and depth, we transition into three-dimensional objects that can be perceived and visualized, such as paper shapes, triangles, or circles. Calculating these dimensions involves starting with a point (or dot) and extending into lines and shapes.

However, the challenge arises when attempting to define a point that lacks dimensions. Even in algorithmic computations, a "point" exists merely as data, and constructing geometric entities using 0-dimensional points—such as infinite lines—proves complex.
The framework of General Relativity is grounded in three-dimensional modeling, creating a mismatch with the concept of 0-dimension. Additionally, subatomic particles, despite being classified as 0-dimensional, exhibit shapes, complicating this definition.
Euclid's principles, dating back to 300 BC, continue to influence physics and other sciences, yet modern studies indicate a need for adaptation. The abstract nature of these concepts may not fully account for the intricacies involved in quantum mechanics or relativity.
Why Continue with Zero Dimensions?
It's crucial to recognize that the 0-dimensional point is a theoretical construct rather than a tangible reality. In the physical world, a true 0-dimensional point does not exist. However, defining it in such a manner can simplify certain complex problems, offering a straightforward approach.
Common Applications of a Null Point:
- In physics, a zero-dimensional point correlates with absolute zero temperature, where molecular motion ceases entirely.
- In algebra, the additive identity is represented by a point with zero dimensions, as adding zero to any value leaves that value unchanged.
- Complex numbers visualize an imaginary axis as a zero-dimensional line, demonstrating that Earth completes a rotation around this axis approximately every 23 hours, 56 minutes, and 4 seconds.
A note on algebra: The multiplicative identity maintains the original number, as multiplying by one yields the same result. Thus, zero is recognized as a real number, negating the concept of total nullity.
My aim is to reframe the first dimension and establish a connection between abstract concepts and reality, allowing us to visualize and compute real-world issues.
Defining the First Dimension: A New Mathematical Perspective
I aspire to create a framework for the ideas and psychological constructs we hold. Abstract concepts permeate our reality, encompassing historical contexts, political divisions, and individual growth. By refining our understanding of the first dimension, we can give form to these abstractions.
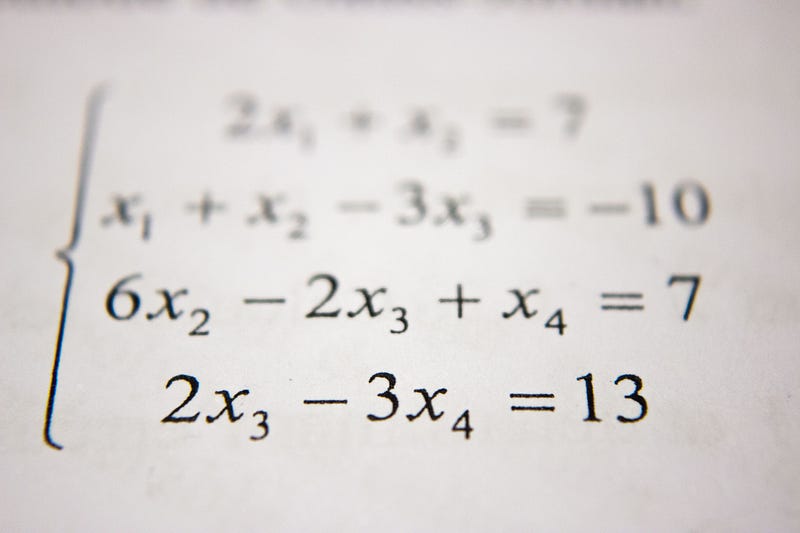
Methods to Define a Point as One-Dimensional:
- Cartesian Coordinates: This system combines algebra and geometry, defining a point as one-dimensional, situated on a specified axis.
- Topology: Here, a point is seen as a space element, representing a one-dimensional manifold that resembles a line. Examples include curves and circles.
- Real Analysis: This approach utilizes real numbers to pinpoint a position on a one-dimensional line, with positive or negative values indicating direction.
Exploring the Point's Reality
Probability theory offers a fascinating perspective on defining points. It assesses the likelihood of an event occurring; if the probability is zero, the event won’t transpire, while a probability of one ensures it does. The probabilities range from 0 to 1, with no negative values.
However, one can also reflect on past experiences—when we forget something and must relearn it. This backward glance might reveal a larger issue manifesting as a concept, necessitating exploration of its origins.
Thus, I propose to merge these ideas: Point A in one-dimensional Cartesian space can be expressed as A(x). If Point A is at position 2, it's represented as A(2); moving in the negative direction is A(-2), and the origin is A(0). Topology will guide our mapping, where a single coordinate, x, identifies Point A.
In Real Analysis, a single real number denotes Point A, visualized on a number line (0,1,2,3,...). The notations A=a and the origin being 0 assist in representing these concepts.
As we delve deeper into Real Analysis, computations illustrating lines as X(a), X(b), and X(0) come into play, with the origin still being X(0).
Future Considerations and Insights
If a point represents the first dimension, what then is the dimension of a line? A line cannot exist without an origin, as Real Analysis illustrates with X(0)—the origin as a real number zero. Notations A(X) or X(0) denote the first dimension.
Together, the origin and line define one another. A line’s existence begins at its origin, similar to how a train starts at the beginning of a track, with the track delineating its path.
The journey to uncover the mathematical foundations for dimensions continues, as I explore interactions between dimensions and cycles. The interplay among two or three dimensions may yield two-dimensional outcomes, yet this does not equate to the second dimension itself.
Mapping abstract ideas alongside tangible realities offers insights into real-world challenges. By revisiting historical patterns, we can forge better societal solutions, addressing political and personal divides through the lenses of biology and psychology. Perhaps we can even guide evolution back to its natural trajectory.
Ingrid Daubechies discusses the foundational aspects of data science, providing a comprehensive overview of key concepts essential for understanding dimensions in mathematics.
In this video, Alex Rosenthal and George Zaidan explore the complexities of dimensions, expanding on the foundational ideas presented in this discussion.