Understanding the Intersection of Parallel Lines in Geometry
Written on
The Evolution of Visual Perception
How can parallel lines intersect when they are defined as maintaining a constant distance? This idea may seem nonsensical at first glance, yet it is not only feasible but essential in both mathematics and science. In this discussion, we will trace the historical evolution of optics and how it leads to the understanding of intersecting parallel lines. We will also delve into practical applications of this intriguing concept.
Understanding Vision
The idea that light rays bounce off objects and enter our eyes is a relatively modern realization. Surprisingly, this notion is not very intuitive. Historical records reveal that many influential thinkers, including Plato and the Pythagoreans, believed that vision was achieved through a fire-like emission from our eyes. Competing theories also existed regarding how our eyes produce light.
The first systematic theory of vision based on reflected light rays was put forth by the mathematician Abu ‘Ali al-Hasan ibn al-Haytham, known in the West as Alhazen, in his seminal work, Kitab al-Manazir. This book was later translated into Latin, leading to a more sophisticated understanding of vision and perspective among European scientists and artists.
Artistic Representation of Parallel Lines
After the establishment of the reflected light theory, European art underwent a significant transformation. Artists began to create more realistic representations of the world around them, realizing that points on their canvas represented lines in three-dimensional space. This understanding implied that parallel lines in their visual field needed to intersect on their canvas.
To clarify this concept, let’s consider the following image:

Imagine you are a Renaissance painter attempting to depict the scene above. According to the reflected light theory, every point in your three-dimensional view creates a line of sight to your eyes. If we denote the train tracks as R1 and R2, each point on these tracks corresponds to a unique line of sight.
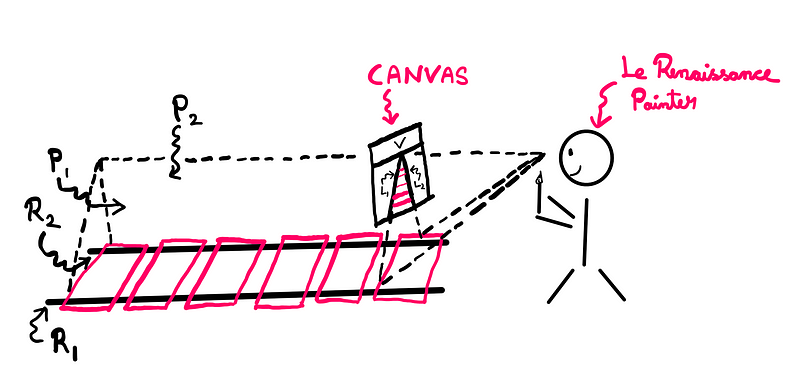
The critical insight here is that while each point on your canvas represents a line in three-dimensional space, each line in that space corresponds to a plane on your canvas. By sweeping a plane through all the lines of sight from your eyes to rail R1, you create a plane P1. A similar process with rail R2 leads to a plane P2.
While the rails R1 and R2 remain parallel, the planes P1 and P2 intersect at your eye, causing the lines L1 and L2 (which represent the rails) to converge at a single point, known as the vanishing point V.
The Mathematics of Vanishing Points
The phenomenon you just encountered as a Renaissance artist is recognized in mathematics as projective geometry. Most of us are accustomed to Euclidean geometry, which makes concepts like projective geometry seem counterintuitive. In projective geometry, parallel lines do intersect!
Returning to the vanishing point, lines L1 and L2 meet at V, and all lines parallel to the tracks in reality will converge at V on your canvas. The only lines that do not converge at a vanishing point are those parallel to the canvas itself, such as the slats between the rails. The train tracks help illustrate this concept, but many more lines of sight originate from our eyes than there are points along the rails.
The term "horizon" becomes clearer in this context. The vanishing point V signifies a location on the horizon that is infinitely distant from your position along the direction of the tracks, referred to mathematically as a "point at infinity." To further explore this idea, let’s examine the projective plane.
The Projective Plane and Infinite Intersections
The plane depicted below resembles the conventional two-dimensional plane you are familiar with, but with some critical differences. Let us consider two points at infinity: P and Q.
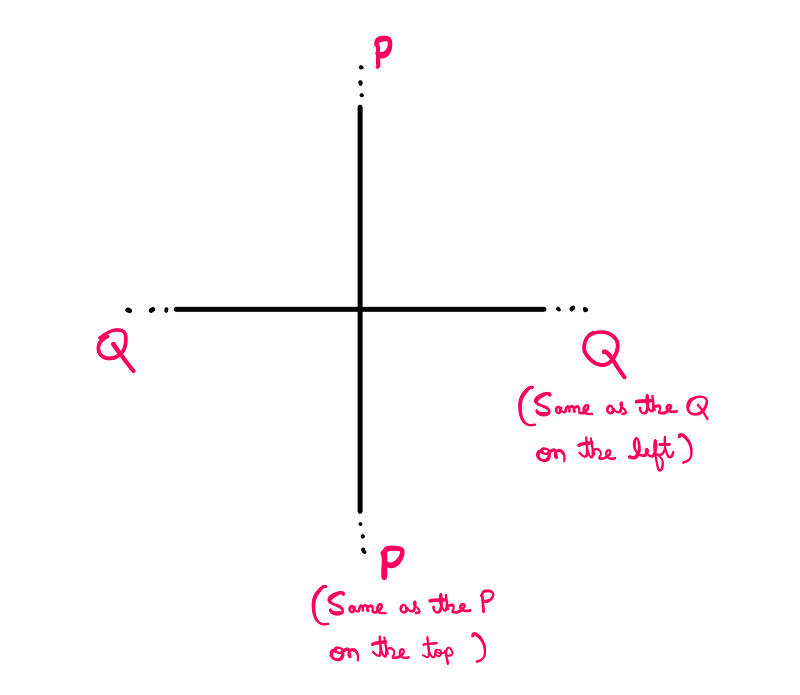
If you travel infinitely in the positive y-direction, you will reach point P. However, this point also represents the same infinitely distant location in the negative y-direction. Continuing in the positive y-direction past P means you are moving towards the origin along the negative y-axis.
This leads to a fascinating conclusion: the vertical axis appears as a circle rather than a straight line in the projective plane. The same holds true for Q along the horizontal direction (x-axis).
In Euclidean geometry, two points determine a line, and two different lines intersect at a unique point—unless they are parallel, in which case they never meet. However, in the projective plane, we eliminate the last condition, adhering to only two principles:
- Each pair of points defines a unique line.
- Each pair of lines intersects at exactly one point.
These axioms hold true without exception, even for parallel lines. In projective geometry, parallel lines simply meet at infinity (think of the vanishing point). Therefore, any line parallel to the vertical axis will also intersect at point P. This understanding aligns well with the concept of poles and lines of longitude.

Final Thoughts
As Jordon Ellenberg aptly states regarding projective plane geometry:
“It’s perfectly symmetrical and elegant in a way that classical plane geometry is not.”
Typically, when a concept in mathematics possesses elegance, scientists eventually find practical applications for it. Conversely, sometimes practical scientific ideas are elegantly represented in the realm of mathematics.
Projective plane geometry proves valuable not only in Renaissance art but also in mapping intricate internet structures for web applications, among other uses. Ultimately, if one is willing to transcend Euclidean perspectives, it becomes evident that parallel lines can indeed intersect. This realization has propelled advancements in scientific fields, such as relativity theory, by encouraging us to look beyond traditional geometric frameworks.
The first video titled "Where Do Parallel Lines Intersect?" dives into the principles and implications of parallel lines in geometry, shedding light on their intersections and how they are perceived in different contexts.
The second video, "Creating a Parallel Line Through a Point Not on the Line," elaborates on the methods of constructing parallel lines and their relevance in various geometric scenarios.