Numerical Simulation Techniques

The relationship between simulation and experimental results is particularly intriguing. One notable paper employs a method known as the density matrix renormalization group (DMRG) algorithm. Within this framework, two parameters can be adjusted: the detuning, denoted by the Greek letter delta, and the blockade radius. By manipulating these variables across a range, we can quantify the bipartite entanglement entropy, S.

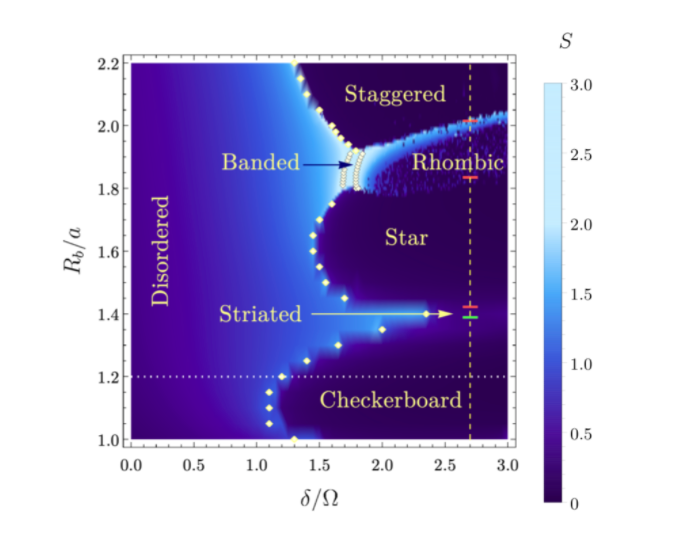
The heat-map depicted above, sourced from [2], illustrates varying degrees of entanglement entropy using a color-coded system. The y-axis represents the blockade length while the x-axis shows the detuning degree. Notably, certain detuning values yield maximum entanglement. Furthermore, by maintaining a constant blockade radius, we can observe phase transitions as we adjust the detuning. For instance, when the blockade radius is fixed at 1.2, represented by the dotted line, increasing the detuning initiates a transition into a checkerboard state.

Density Matrix Renormalization Group (DMRG)

In my earlier discussion, I described the Hamiltonian governing these systems. To identify the ground state, we utilize DMRG, limiting interactions to closely situated atoms. This method operates by focusing on the ground state of a small atom block and iteratively expanding to larger configurations. It currently stands as the most accurate algorithm for computing ground states.

To illustrate this concept, let's consider a simple model: a chain of atoms that can be in either a spin-up or spin-down state. The Hamiltonian governing this spin chain includes a term that dictates interactions between adjacent atoms. Here, S represents the spin operator, which has three components due to its vector nature.

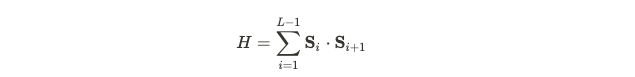
For extensive systems, diagonalizing this Hamiltonian becomes nearly impossible, necessitating numerical methods to extract the low-energy physics of interest.

Understanding Entanglement Entropy

Entanglement entropy quantifies the level of quantum entanglement between two systems. A high entanglement entropy indicates a strong entanglement between the systems. Mathematically, if we divide a quantum system into two components A and B, we can describe these components using distinct Hilbert spaces. For example, splitting an array of atoms into two halves allows us to assign the left half to Hilbert space A and the right half to Hilbert space B.

Typically, the overall Hilbert space can be expressed as the tensor product of these two systems. A tensor product is a formal mechanism for combining two spaces, effectively capturing the quantum mechanics of the systems involved.

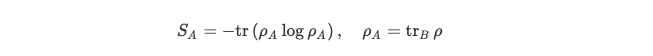
The formula for entanglement entropy is constructed from our quantum state's density matrix, denoted as rho. By tracing out one half of the space, we can compute the resulting entropy.

An Overview of Density Matrices

How do we initially describe quantum states? Exact quantum states can be expressed as linear combinations of basis states within our Hilbert space, accompanied by known coefficients. However, when measuring, it can be challenging to ascertain the precise quantum states being prepared. This complexity arises partly due to the nature of the system being measured, such as a lattice of atoms, and the interactions with the measuring devices, which themselves consist of numerous atoms.

To account for uncertainties in quantum systems, we represent them with a density operator. The rho_i values indicate our prior probabilities concerning a given quantum system's state. This representation embodies our perspective as experimenters regarding the actual quantum state.

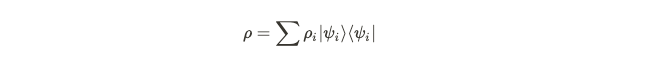
It’s essential to note that this does not assert what the precise quantum state is. In exact probability amplitude calculations, the state is defined as a linear combination of eigenvectors of the observable. Though this combination includes probabilities for various observable quantities, the quantum state remains 'definite' and pure. The coefficients differ from the rho_i prior probabilities mentioned earlier, highlighting a philosophical distinction in using a density matrix compared to merely summing linear combinations of basis states.