Engage Your Mind with This Intriguing Probability Challenge
Written on
Chapter 1: Exploring the World of Probability
Probability puzzles are among the most stimulating and enjoyable exercises for the mind. Here’s a challenge to test your skills…

One of my favorite pastimes is collaborating with bright high school students, preparing them for the rigors of mathematics and statistics at the university level. This experience deepens my understanding of fundamental concepts, enabling me to teach them more effectively. I also take pleasure in discovering engaging and complex problems that truly challenge students to expand their comprehension of basic principles into advanced concepts.
Probability is one of the most straightforward yet intriguing areas of mathematics. Despite its simple foundation, it can lead to some perplexing and challenging questions. Here’s a recent example of a demanding probability exam question. I’ll share the entire problem, and I encourage you to attempt it before moving on to see my approach.
The Problem

This problem is structured to help you ease into it, starting with some simple preliminary questions before gradually challenging you to think about various scenarios, ultimately leading you to draw broad conclusions. As you work through this problem, consider how each step sets the stage for the next.
My Solutions — Initial Steps
The first parts (a), (b), and (c) serve as warm-ups to get you thinking in the right direction.
- A complete tournament cannot occur since no player has won consecutive matches.
- This scenario is impossible because Player B lost the first match and thus cannot compete in or win the second match.
- This scenario is a complete tournament, where Player A defeats Player B, Player C defeats Player A, Player B defeats Player C, and Player B defeats Player A.
The purpose of these initial questions is to suggest a methodology—specifically, to examine sequences of letters and determine which combinations are feasible.
My Solutions — Middle Steps
The middle section explores what could transpire in the initial five games. It starts by asking for the probability that no player wins within those games. There are two sequences: ACBAC or BCABC, each with a probability of (1/2)?, resulting in a total probability of (1/2)? = 1/16.
Next, it inquires about the probability that Player A wins within five games. There are three sequences: AA, ACBAA, and BCAA. Therefore, the total probability is (1/2)² + (1/2)? + (1/2)? = 11/32.
We can expect similar outcomes for Player B. Here, the sequences are: BB, BCABB, and ACBB—again summing to 11/32.
Player C presents a different situation since they cannot participate in the first match. Thus, the ways Player C can win within five games are ACC or BCC, leading to a probability of 2 x (1/2)³ = 1/4.
To verify our findings, we can perform a checksum, expecting that either Player A, Player B, or Player C will win within five games, or nobody wins. Thus, 11/32 + 11/32 + 1/4 + 1/16 = (11 + 11 + 8 + 2)/32 = 1, which confirms our calculations.
My Solutions — Final Steps
At this stage, we are asked to extend our observations to the limit. Let’s analyze the probability that Player A wins at some point. If AA occurs, they win immediately. If not, the only other initial possibilities are AC or BC.
Assuming we start with AC, the next winning combination for A would be ACBAA, followed by ACBACBAA, then ACBACBACBAA, resulting in lengths of 5, 8, 11, etc. Including AA, these lengths can be expressed as a series: 3k-1 for positive integer values of k.
If we start with BC, the next winning sequence for A would be BCAA, followed by BCABCAA, then BCABCABCAA, resulting in lengths of 4, 7, 10, etc. This series can be expressed as 3k + 1 for positive integer values of k.
Consequently, we determine that the probability of Player A winning at some point is:
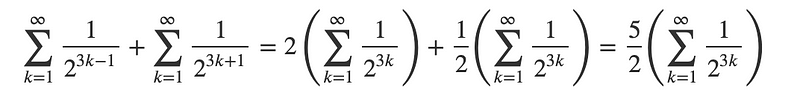
Using the formula for the sum of an infinite series, with an initial term of (1/2)³ = 1/8 and a ratio of (1/2³) = 1/8, we find that the infinite sum equals 1/7. Therefore, our final answer is (5/2)*(1/7) = 5/14 as required.
Similarly, since the probability of Player B winning at some point parallels that of Player A, we conclude that the probability of Player B winning is also 5/14.
Since the only remaining possibility is Player C winning, we calculate that the probability of Player C winning at some point is 1 - P(B wins) - P(A wins) = 1 - 10/14 = 4/14 = 2/7.
To confirm the result for Player C's victory: Since Player C cannot win in the first game, we recognize two equivalent paths for Player C to win at some point, depending on who wins the first game. The sequences are either ACC, ACBACC, ACBACBACC, etc., or BCC, BCABCC, BCABCABCC, etc. Thus, we have two series of length 3k.
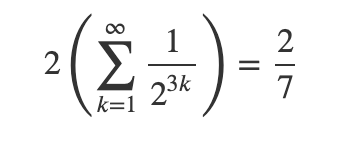
I hope you found this challenge enjoyable. Feel free to share your thoughts on how you approached it or your reactions to the solution.
Explore the intriguing world of probability with this brain teaser that will test your mathematical skills.
Check out this video for a detailed explanation of the probability quiz and enhance your understanding of the topic.